Educación Tecnológica - Esc. Industrial N°2
Tecnología y Necesidad

¿Alguna vez se preguntaron cómo es que un celular puede hacer tantas cosas o cómo un puente gigante se mantiene en pie? La respuesta está en la unión de tres fuerzas poderosas: la ciencia, la técnica y la tecnología. ¡Vamos a explorarlas!
¿Qué es la Ciencia?
- La ciencia es como un detective curioso que siempre está preguntando "¿por qué?". Busca entender cómo funciona el mundo que nos rodea, desde las cosas más pequeñas como los átomos, hasta las más grandes como las estrellas.
- Los científicos hacen experimentos, observan y crean teorías para explicar los fenómenos naturales. Por ejemplo, Isaac Newton descubrió la ley de la gravedad al observar cómo caían las manzanas.
- La ciencia nos da el "conocimiento" sobre cómo funcionan las cosas.
- La técnica es el "cómo hacer" las cosas. Son los pasos y las habilidades que usamos para construir o crear algo.
- Un carpintero que construye una silla, un cocinero que prepara una pizza o un mecánico que arregla un auto, todos usan técnicas.
- La técnica se aprende con la práctica y la experiencia.
- La tecnología es una actividad humana, creativa y organizada. Es la forma en que nosotros, los seres humanos, usamos nuestro ingenio y conocimiento para transformar el mundo que nos rodea.
- Utilizamos el conocimiento que nos da la ciencia y las habilidades que aprendemos con la técnica para crear herramientas, máquinas, sistemas y procesos.
- El objetivo principal de la tecnología es resolver problemas, satisfacer necesidades y mejorar nuestra calidad de vida.
- La tecnología no solo se trata de objetos físicos como celulares o computadoras, sino también de procesos y sistemas, como la forma en que organizamos el transporte público o cómo producimos alimentos.
- Es importante resaltar que la tecnología está en constante evolución, siempre buscando nuevas y mejores formas de hacer las cosas.
- La ciencia descubre: Los científicos descubren nuevos conocimientos sobre el mundo.
- La técnica aplica: Los técnicos usan esos conocimientos para desarrollar métodos y herramientas.
- La tecnología crea: Los ingenieros y diseñadores combinan la ciencia y la técnica para crear productos tecnológicos que satisfacen nuestras necesidades.
- Comunicarnos a distancia.
- Ciencia: Descubrimiento de las ondas electromagnéticas.
- Técnica: Desarrollo de circuitos electrónicos y antenas.
- Tecnología: Creación de celulares y redes de comunicación.
- Cruzar un río.
- Ciencia: Estudio de la resistencia de materiales y la mecánica de estructuras.
- Técnica: Desarrollo de técnicas de construcción de puentes.
- Tecnología: Construcción de puentes colgantes o atirantados.
- Obtener agua potable.
- Ciencia: Estudiamos las propiedades del agua y cómo eliminar impurezas.
- Técnica: Desarrollamos métodos de filtración y purificación.
- Tecnología: Construimos plantas de tratamiento de agua y sistemas de distribución para llevar agua limpia a nuestras casas.
Ejemplo: imagina que vas paseando por el campo, y quieres cruzar un arroyo sin mojarte los pies.
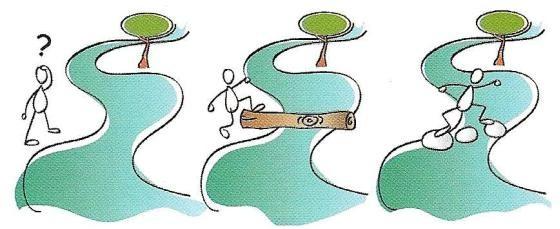 Pregunta: ¿Cómo lo cruzarías? Teníamos un problema o necesidad, que hemos solucionado utilizando nuestra imaginación y conocimientos para desarrollar un objeto que ha resuelto el problema, esto es, la Tecnología.
Pregunta: ¿Cómo lo cruzarías? Teníamos un problema o necesidad, que hemos solucionado utilizando nuestra imaginación y conocimientos para desarrollar un objeto que ha resuelto el problema, esto es, la Tecnología.En ocasiones el problema se resuelve con la realización de un objeto muy sencillo (una silla para sentarnos, un lápiz para escribir), y en otras ocasiones el problema se resuelve con un producto muy sofisticado (un radiotelescopio para estudiar el universo).
En todos los casos, se está haciendo Tecnología.
A lo largo de la historia el ser humano ha tenido ingeniárselas para encontrar soluciones a los diferentes problemas que les iban surgiendo, y satisfacer con ello sus necesidades y deseos (como la salud, el vestido, la alimentación, la vivienda, la comunicación, el transporte, etc.).
El resultado es la multitud de productos creados, desde un cepillo de dientes o un lápiz, hasta un ordenador o una estación espacial.
NECESIDADES DEL SER HUMANO.
Necesidades básicas:
Son las necesidades imprescindibles que el ser humano necesita cubrir para poder sobrevivir. Se trata de la alimentación, el vestido, la vivienda y la salud.
Alimentación: la necesidad de alimentarse provocó el desarrollo de instrumentos que facilitaron la caza, la pesca, la agricultura y la ganadería.
Vestido: los humanos primitivos se vestían con pieles de animales unidas con cuero, huesos, etc. En la actualidad se disponen de prendas fabricadas con materiales y diseños modernos.
Vivienda: La necesidad de buscar refugio frente las inclemencias del tiempo se han ido solventando mediante la construcción de viviendas, desde las primeras cavernas y chozas, hasta los actuales edificios equipados con todo tipo de utensilios de cocina, calefacción, agua, electrodomésticos, etc.
Salud: para prevenir y curar enfermedades se han desarrollado productos tecnológicos que permiten diagnosticar enfermedades, realizar operaciones, tratar dolencias, etc.

Necesidades secundarias:
Se trata de otras necesidades distintas de las básicas, que en la sociedad actual también cobran gran importancia.
Seguridad: para garantizar la seguridad en vehículos, en el trabajo, en casa, etc. la Tecnología ha desarrollado diversos productos.
Comunicación: la comunicación de información ha utilizado soluciones como campanas, señales de humo, correo, telégrafo, etc.
En la actualidad la comunicación ha experimentado una importante revolución gracias a la radio, la TV, Internet, teléfonos móviles, etc.
Transporte: el comercio y el turismo suponen la necesidad de transportar personas y mercancías. Para ello la tecnología desarrolló la rueda, el carro, los barcos, automóviles, carreteras, puentes, etc.
Trabajo: el ser humano ha desarrollado multitud de útiles, herramientas y máquinas que han facilitado el trabajo. Con estos dispositivos se consigue hacer más fáciles ciertas tareas que de otro modo resultarían lentas, duras y difíciles de llevar a cabo.
Ocio: la necesidad de descansar, distraerse y divertirse siempre ha estado presente. Algunas de las respuestas de la Tecnología han sido los juguetes, juegos, instrumentos musicales, cine, atracciones, etc.





Productos Tecnologicos

Los productos tecnológicos son el resultado de la actividad tecnológica. La Tecnología se concreta en los productos tecnológicos que responden a demandas de la sociedad. Todo procedimiento tecnológico tiende a producir un producto para satisfacer alguna necesidad. Los productos tecnológicos se clasifican en Bienes o Servicios.
Los Bienes son objetos materiales tangibles, es decir, se pueden tocar. Tienen la característica que primero se producen y luego se usan.
El hecho que se llamen “bienes” no significa que “nos hagan bien”. Por ejemplo, un cigarrillo o una bomba atómica son bienes (porque se pueden tocar y están hechos por el hombre), aunque no nos hagan ningún bien.
Son ejemplos de bienes: una silla, una mesa, una computadora, un celular, un corcho, etc.
|
|
|
|
Los Servicios son acciones o prestaciones inmateriales que se brindan para satisfacer una necesidad. Son intangibles, es decir, no se pueden tocar.
Tienen la característica que se producen y se usan al mismo tiempo. Por ejemplo, cuando utilizamos el transporte público, dicho servicio se produce y lo utilizamos al mismo instante (cuando nos subimos al colectivo).
Como ejemplos de servicios, además del transporte, podemos nombrar la educación, la atención médica, el suministro de electricidad, etc.
|
|
|
|
¿Se han preguntado alguna vez si la ciencia, la técnica y la tecnología tienen alguna relación?
Para conocer que relación existe entre estos tres conceptos es necesario definir qué es la ciencia, y qué es la técnica. Sólo veremos unas breves definiciones porque para profundizar en el tema necesitaríamos mucho más tiempo.
Vamos a decir que la Ciencia es un conjunto de conocimientos aceptados como verdaderos.
 Y Técnica es un procedimiento, una serie de pasos que realiza una persona con un objetivo determinado.Históricamente Ciencia y Técnica caminaron separadamente. La ciencia siempre estuvo ligada a personas con acceso a medios escritos, que normalmente eran de una clase social elevada. En cambio, la técnica era patrimonio de los artesanos, que realizaban procedimientos sin conocer la explicación y fundamentación teórica de sus actos.
Y Técnica es un procedimiento, una serie de pasos que realiza una persona con un objetivo determinado.Históricamente Ciencia y Técnica caminaron separadamente. La ciencia siempre estuvo ligada a personas con acceso a medios escritos, que normalmente eran de una clase social elevada. En cambio, la técnica era patrimonio de los artesanos, que realizaban procedimientos sin conocer la explicación y fundamentación teórica de sus actos.La Tecnología es una actividad que une estos dos conceptos. A la hora de la realización de productos para satisfacer alguna necesidad, la Tecnología utiliza los conocimientos provenientes de la Ciencia, y los procedimientos (pasos a seguir) de la Técnica.
Energía

La energía
1.- Introducción
La energía está presente en todos los fenómenos que ocurren en el Universo.
La energía es una propiedad de los cuerpos. Es algo que poseen todos los cuerpos del
Universo y que tiene varias características:
Permite producir cambios en los cuerpos (como el aumento de temperatura de un vaso de leche en el microondas).
Puede ser transformada de una a otra (como la energía solar que se transforma en energía calorífica en las placas solares).
Puede ser transferida de uno a otro cuerpo (si ponemos es contacto dos barras de hierro a diferente temperatura, la más caliente le transfiere ese calor a la más fría).
Todas las formas de energía son intercambiables entre sí.
El ser humano explota los recursos naturales (carbón, petróleo, viento, sol, agua, etc.) y obtiene de ellos energía para usarla directamente o para transformarla en otra más adecuada para su uso.
2.- Formas de energía
Energía calorífica o térmica
Es la energía asociada a la temperatura y relacionada con el calor.
La energía calorífica es la liberada por los cuerpos más calientes en forma de calor y pasa a los cuerpos más fríos.
Ejemplo…
Si tocamos un vaso de leche caliente, el calor pasa a nuestra mano, que está más fría.
Energía cinética
Es la energía asociada a la velocidad que tienen los cuerpos. Cuanto más rápido, más
energía cinética se posee.
Ejemplo…
Si una pelota de golf nos golpea en la cabeza, está claro que nos hará más daño
cuánta más velocidad tenga la pelota.
Energía eléctrica
Esta es la energía más familiar para nosotros. La usamos prácticamente a todas horas y
en casi todas nuestras actividades. Esta energía es tan usada por varias razones:
Es fácil de obtener a partir de otras formas de energía.
Es fácil de transportar a grandes distancias.
Es fácil de transformar en otros tipos de energía.
Energía eólica
Es la energía cinética del viento (el dios griego del viento era Eolo). La energía eólica se puede usar directamente, como para impulsar barcos de vela, y también se puede usar para transformarla en energía eléctrica mediante aerogeneradores.
Energía geotérmica
El interior de la Tierra conserva gran cantidad de calor
desde los tiempos en que se formó, los volcanes dan buena
prueba de ello. En algunas zonas de la corteza terrestre, este
calor aflora a la superficie y constituye lo que llamamos
energía geotérmica.
Se trata de una energía calorífica que constituye un interesante
recurso natural como fuente de energía.
Energía hidráulica
Llamamos así a la energía que posee el agua por el simple
hecho de moverse. Tanto en saltos naturales como en saltos
de agua artificiales, como los que el ser humano construye en
los embalses.
A veces se aprovecha directamente, por ejemplo para mover
una noria. Otras veces se aprovecha para transformarla en
energía eléctrica.
Energía luminosa
Es la energía asociada a la luz. El Sol desprende gran cantidad de esta energía, pero
también una bombilla o una vela encendida.
La energía luminosa es una clase de otra forma de energía más amplia, la energía
electromagnética, que ya estudiaremos más adelante.
Energía mareomotriz
La energía mareomotriz es la asociada al movimiento de
las olas, y al de las mareas.
Es una energía asociada al movimiento, por tanto se trata de
una energía cinética.
Energía nuclear
Es la energía almacenada en el núcleo de los átomos. Esta
energía se libera cuando se rompen los núcleos de los átomos,
proceso al que se llama fisión nuclear.
La energía nuclear que aprovechamos los seres humanos se libera
mediante reacciones nucleares de fisión provocadas artificialmente.
Los átomos que suelen emplearse en estas reacciones son de uranio.
Energía potencial elástica
Es la energía asociada a la deformación de los
cuerpos elásticos, los que recuperan su forma original
cuando la fuerza que los ha deformado deja de actuar.
Cuando un muelle se comprime o se estira, almacena
energía potencial elástica, pero cuando el muelle recupera
su forma, pierde esta energía almacenada.
La cuerda tensa del arco tiene energía
Energía potencial gravitatoria
Es la energía asociada a la altura a la que se encuentra un
cuerpo respecto a la superficie de la Tierra.
Cuando un cuerpo gana altura almacena energía potencial
gravitatoria, esta energía se libera cuando el cuerpo cae o pierde
altura (cuanto más alto subas, mayor es la torta que te das).
Cuando el cuerpo cae, gana velocidad, la energía potencial se
transforma en energía cinética.
Energía química
Es la energía liberada en las reacciones químicas. Se produce
cuando los enlaces atómicos se rompen y estos se combinan
formando nuevos productos.
Hay reacciones químicas cuando el motor del coche quema
gasolina. En este caso la energía química del combustible se
transforma en energía cinética del coche.
En el interior de nuestro organismo hay una continua utilización de la energía química
acumulada en los alimentos, que es transformada en energía metabólica por nuestras
células, lo que nos permite vivir.
No todos los alimentos tienen almacenada la misma cantidad de energía química, por eso
no todos tienen las mismas calorías.
Energía sonora
La energía sonora está asociada a las ondas sonoras que
se transmiten a través del aire, también pueden hacerlo a
través de cualquier sustancia, pero en el vacío. El sonido
necesita un soporte físico para poder transmitirse.
El mecanismo de transmisión de la energía sonora es
aproximadamente así:
Las partículas del aire reciben un choque (por ejemplo, el
producido por la vibración de un altavoz de la radio, o el sonar
de un barco). Debido al choque empiezan a vibrar, chocan con
otra partícula y le pasan la vibración, volviendo a su sitio.
Energía solar
Es la energía radiante del Sol. Llega hasta nosotros en forma
de ondas electromagnéticas: luz visible, microondas, rayos X,
rayos ultravioleta, etc.
La energía solar es la fuente de la que emana la mayoría de la
energía de la que podemos disponer en la Tierra.
La energía solar tiene su origen en reacciones nucleares de
fusión, que se producen en el interior del Sol, iguales que las
que ocurren en todas las estrellas.
La energía solar se utiliza tanto directamente como para transformarla en energía eléctrica
o térmica.
Tantos tipos de energía y todos se resumen en dos…
Hemos visto varias formas de energía, y podríamos seguir viendo más, pero todas ellas se
pueden agrupar en dos grandes formas:
La energía cinética
La energía potencial
Porque, al fin y al cabo, cualquier forma de energía depende o bien de la posición del
cuerpo (energía potencial) o del movimiento del cuerpo (energía cinética).
1.- Introducción
La energía está presente en todos los fenómenos que ocurren en el Universo.
La energía es una propiedad de los cuerpos. Es algo que poseen todos los cuerpos del
Universo y que tiene varias características:
Permite producir cambios en los cuerpos (como el aumento de temperatura de un vaso de leche en el microondas).
Puede ser transformada de una a otra (como la energía solar que se transforma en energía calorífica en las placas solares).
Puede ser transferida de uno a otro cuerpo (si ponemos es contacto dos barras de hierro a diferente temperatura, la más caliente le transfiere ese calor a la más fría).
Todas las formas de energía son intercambiables entre sí.
El ser humano explota los recursos naturales (carbón, petróleo, viento, sol, agua, etc.) y obtiene de ellos energía para usarla directamente o para transformarla en otra más adecuada para su uso.
2.- Formas de energía
Energía calorífica o térmica
Es la energía asociada a la temperatura y relacionada con el calor.
La energía calorífica es la liberada por los cuerpos más calientes en forma de calor y pasa a los cuerpos más fríos.
Ejemplo…
Si tocamos un vaso de leche caliente, el calor pasa a nuestra mano, que está más fría.
Energía cinética
Es la energía asociada a la velocidad que tienen los cuerpos. Cuanto más rápido, más
energía cinética se posee.
Ejemplo…
Si una pelota de golf nos golpea en la cabeza, está claro que nos hará más daño
cuánta más velocidad tenga la pelota.
Energía eléctrica
Esta es la energía más familiar para nosotros. La usamos prácticamente a todas horas y
en casi todas nuestras actividades. Esta energía es tan usada por varias razones:
Es fácil de obtener a partir de otras formas de energía.
Es fácil de transportar a grandes distancias.
Es fácil de transformar en otros tipos de energía.
Energía eólica
Es la energía cinética del viento (el dios griego del viento era Eolo). La energía eólica se puede usar directamente, como para impulsar barcos de vela, y también se puede usar para transformarla en energía eléctrica mediante aerogeneradores.
Energía geotérmica
El interior de la Tierra conserva gran cantidad de calor
desde los tiempos en que se formó, los volcanes dan buena
prueba de ello. En algunas zonas de la corteza terrestre, este
calor aflora a la superficie y constituye lo que llamamos
energía geotérmica.
Se trata de una energía calorífica que constituye un interesante
recurso natural como fuente de energía.
Energía hidráulica
Llamamos así a la energía que posee el agua por el simple
hecho de moverse. Tanto en saltos naturales como en saltos
de agua artificiales, como los que el ser humano construye en
los embalses.
A veces se aprovecha directamente, por ejemplo para mover
una noria. Otras veces se aprovecha para transformarla en
energía eléctrica.
Energía luminosa
Es la energía asociada a la luz. El Sol desprende gran cantidad de esta energía, pero
también una bombilla o una vela encendida.
La energía luminosa es una clase de otra forma de energía más amplia, la energía
electromagnética, que ya estudiaremos más adelante.
Energía mareomotriz
La energía mareomotriz es la asociada al movimiento de
las olas, y al de las mareas.
Es una energía asociada al movimiento, por tanto se trata de
una energía cinética.
Energía nuclear
Es la energía almacenada en el núcleo de los átomos. Esta
energía se libera cuando se rompen los núcleos de los átomos,
proceso al que se llama fisión nuclear.
La energía nuclear que aprovechamos los seres humanos se libera
mediante reacciones nucleares de fisión provocadas artificialmente.
Los átomos que suelen emplearse en estas reacciones son de uranio.
Energía potencial elástica
Es la energía asociada a la deformación de los
cuerpos elásticos, los que recuperan su forma original
cuando la fuerza que los ha deformado deja de actuar.
Cuando un muelle se comprime o se estira, almacena
energía potencial elástica, pero cuando el muelle recupera
su forma, pierde esta energía almacenada.
La cuerda tensa del arco tiene energía
Energía potencial gravitatoria
Es la energía asociada a la altura a la que se encuentra un
cuerpo respecto a la superficie de la Tierra.
Cuando un cuerpo gana altura almacena energía potencial
gravitatoria, esta energía se libera cuando el cuerpo cae o pierde
altura (cuanto más alto subas, mayor es la torta que te das).
Cuando el cuerpo cae, gana velocidad, la energía potencial se
transforma en energía cinética.
Energía química
Es la energía liberada en las reacciones químicas. Se produce
cuando los enlaces atómicos se rompen y estos se combinan
formando nuevos productos.
Hay reacciones químicas cuando el motor del coche quema
gasolina. En este caso la energía química del combustible se
transforma en energía cinética del coche.
En el interior de nuestro organismo hay una continua utilización de la energía química
acumulada en los alimentos, que es transformada en energía metabólica por nuestras
células, lo que nos permite vivir.
No todos los alimentos tienen almacenada la misma cantidad de energía química, por eso
no todos tienen las mismas calorías.
Energía sonora
La energía sonora está asociada a las ondas sonoras que
se transmiten a través del aire, también pueden hacerlo a
través de cualquier sustancia, pero en el vacío. El sonido
necesita un soporte físico para poder transmitirse.
El mecanismo de transmisión de la energía sonora es
aproximadamente así:
Las partículas del aire reciben un choque (por ejemplo, el
producido por la vibración de un altavoz de la radio, o el sonar
de un barco). Debido al choque empiezan a vibrar, chocan con
otra partícula y le pasan la vibración, volviendo a su sitio.
Energía solar
Es la energía radiante del Sol. Llega hasta nosotros en forma
de ondas electromagnéticas: luz visible, microondas, rayos X,
rayos ultravioleta, etc.
La energía solar es la fuente de la que emana la mayoría de la
energía de la que podemos disponer en la Tierra.
La energía solar tiene su origen en reacciones nucleares de
fusión, que se producen en el interior del Sol, iguales que las
que ocurren en todas las estrellas.
La energía solar se utiliza tanto directamente como para transformarla en energía eléctrica
o térmica.
Tantos tipos de energía y todos se resumen en dos…
Hemos visto varias formas de energía, y podríamos seguir viendo más, pero todas ellas se
pueden agrupar en dos grandes formas:
La energía cinética
La energía potencial
Porque, al fin y al cabo, cualquier forma de energía depende o bien de la posición del
cuerpo (energía potencial) o del movimiento del cuerpo (energía cinética).
Resistencias en serie
Resistencias en Serie
Todos los circuitos conectados en serie presentan las siguientes características:
En serie la intensidad de corriente en cada resistencia es la misma, es decir: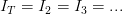
En serie la resistencia total del circuito es igual a la suma de todas las resistencias.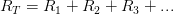
En serie la diferencia de potencial es igual a la suma de las diferencias de potenciales de cada resistencia.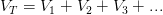
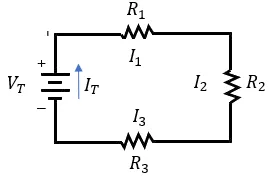
Pero para comprender mejor el tema, es necesario resolver algunos ejercicios, veamos entonces:
Ejercicios Resueltos de Suma de Resistencias
1.- Las resistencias de 6Ω, 8Ω y 12Ω se conectan en serie. ¿Cuál es la resistencia total del circuito?Solución:
Colocando los datos que nos da el problema:
R1 = 6Ω
R2 = 8Ω
R3 = 12Ω
En un circuito en serie, las resistencias se suman, entonces:
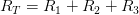 Sustituyendo nuestros datos en la fórmula:
Sustituyendo nuestros datos en la fórmula: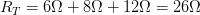 Resultado:Por lo que obtenemos una resistencia equivalente o total de 26Ω
Resultado:Por lo que obtenemos una resistencia equivalente o total de 26Ω
Problema 2.- Dos resistencias 7Ω y 5Ω se conectan en serie a una diferencia de potencial de 120 volts. ¿Cuál es la intensidad de corriente que circula por las resistencias?
Solución:
Anotamos nuestros datos:
R1 = 7Ω
R2 = 5Ω
V = 120V
Rt = ?
It = ?
Al estar en serie las resistencias, calculamos la resistencia equivalente o total, sumando las dos resistencias.
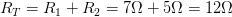 Y ya con ello podemos proceder para poder calcular la intensidad de corriente, de la siguiente forma:
Y ya con ello podemos proceder para poder calcular la intensidad de corriente, de la siguiente forma: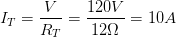 Las resistencias al estar colocadas en serie, poseen la misma corriente cada una.Resultado:
Las resistencias al estar colocadas en serie, poseen la misma corriente cada una.Resultado:
Por lo que la corriente o intensidad es de 12A
Problema 3.- En el circuito siguiente, las resistencias R1, R2, y R3 tienen un valor de 4Ω, 6Ω, y 2Ω respectivamente. Si se le aplican 24V al circuito, encontrar: a) la resistencia total, b) la corriente total y la corriente en cada una de las resistencias, c) el voltaje en cada una de las resistencias.
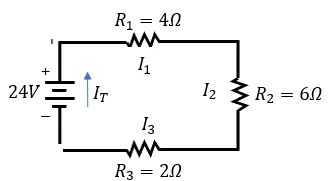
Solución:Procedemos a realizar lo que nos pide cada inciso, partiendo de la resistencia total, la corriente total y en cada una de las resistencias y finalmente el voltaje en cada una de ellas.
a) Resistencia total:
Al estar en serie, tenemos que sumar todas de manera directa, de la siguiente forma:
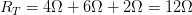 Por lo que obtenemos, un valor total de 12Ωb) Corriente total y corriente en cada resistencia:
Por lo que obtenemos, un valor total de 12Ωb) Corriente total y corriente en cada resistencia:
Al ser un circuito en serie, la corriente es igual en cada una de ellas, entonces aplicamos la ley del ohm.
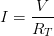 Sustituyendo nuestros datos:
Sustituyendo nuestros datos: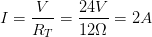 Entonces, la corriente que hay en cada resistencia es de 2 Amperes.c) Voltaje en cada resistencia:
Entonces, la corriente que hay en cada resistencia es de 2 Amperes.c) Voltaje en cada resistencia:
Nuevamente tenemos que recurrir a la Ley del Ohm, para poder calcular el voltaje en cada resistencia, ya que los voltajes si son diferentes en cada componente.
Para la primer resistencia:
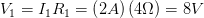 Para la segunda resistencia:
Para la segunda resistencia: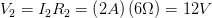 y finalmente para la tercer resistencia:
y finalmente para la tercer resistencia: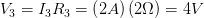 Podemos comprobar si nuestros cálculos son verídicos, ya que si sumamos cada diferencia de potencial en cada resistencia, nos debe dar el valor de la fuente principal, es decir:
Podemos comprobar si nuestros cálculos son verídicos, ya que si sumamos cada diferencia de potencial en cada resistencia, nos debe dar el valor de la fuente principal, es decir: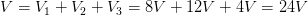
Todos los circuitos conectados en serie presentan las siguientes características:
- 1 Características de las Resistencias en Serie
- 2 Ejercicios Resueltos de Suma de Resistencias en Serie
En serie la intensidad de corriente en cada resistencia es la misma, es decir:
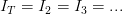
En serie la resistencia total del circuito es igual a la suma de todas las resistencias.
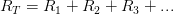
En serie la diferencia de potencial es igual a la suma de las diferencias de potenciales de cada resistencia.
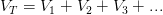

Pero para comprender mejor el tema, es necesario resolver algunos ejercicios, veamos entonces:
Ejercicios Resueltos de Suma de Resistencias
1.- Las resistencias de 6Ω, 8Ω y 12Ω se conectan en serie. ¿Cuál es la resistencia total del circuito?Solución:
Colocando los datos que nos da el problema:
R1 = 6Ω
R2 = 8Ω
R3 = 12Ω
En un circuito en serie, las resistencias se suman, entonces:
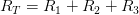 Sustituyendo nuestros datos en la fórmula:
Sustituyendo nuestros datos en la fórmula: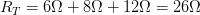 Resultado:Por lo que obtenemos una resistencia equivalente o total de 26Ω
Resultado:Por lo que obtenemos una resistencia equivalente o total de 26ΩProblema 2.- Dos resistencias 7Ω y 5Ω se conectan en serie a una diferencia de potencial de 120 volts. ¿Cuál es la intensidad de corriente que circula por las resistencias?
Solución:
Anotamos nuestros datos:
R1 = 7Ω
R2 = 5Ω
V = 120V
Rt = ?
It = ?
Al estar en serie las resistencias, calculamos la resistencia equivalente o total, sumando las dos resistencias.
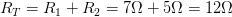 Y ya con ello podemos proceder para poder calcular la intensidad de corriente, de la siguiente forma:
Y ya con ello podemos proceder para poder calcular la intensidad de corriente, de la siguiente forma: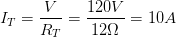 Las resistencias al estar colocadas en serie, poseen la misma corriente cada una.Resultado:
Las resistencias al estar colocadas en serie, poseen la misma corriente cada una.Resultado:Por lo que la corriente o intensidad es de 12A
Problema 3.- En el circuito siguiente, las resistencias R1, R2, y R3 tienen un valor de 4Ω, 6Ω, y 2Ω respectivamente. Si se le aplican 24V al circuito, encontrar: a) la resistencia total, b) la corriente total y la corriente en cada una de las resistencias, c) el voltaje en cada una de las resistencias.

Solución:Procedemos a realizar lo que nos pide cada inciso, partiendo de la resistencia total, la corriente total y en cada una de las resistencias y finalmente el voltaje en cada una de ellas.
a) Resistencia total:
Al estar en serie, tenemos que sumar todas de manera directa, de la siguiente forma:
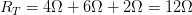 Por lo que obtenemos, un valor total de 12Ωb) Corriente total y corriente en cada resistencia:
Por lo que obtenemos, un valor total de 12Ωb) Corriente total y corriente en cada resistencia:Al ser un circuito en serie, la corriente es igual en cada una de ellas, entonces aplicamos la ley del ohm.
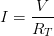 Sustituyendo nuestros datos:
Sustituyendo nuestros datos: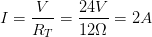 Entonces, la corriente que hay en cada resistencia es de 2 Amperes.c) Voltaje en cada resistencia:
Entonces, la corriente que hay en cada resistencia es de 2 Amperes.c) Voltaje en cada resistencia:Nuevamente tenemos que recurrir a la Ley del Ohm, para poder calcular el voltaje en cada resistencia, ya que los voltajes si son diferentes en cada componente.
Para la primer resistencia:
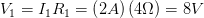 Para la segunda resistencia:
Para la segunda resistencia: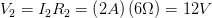 y finalmente para la tercer resistencia:
y finalmente para la tercer resistencia: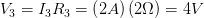 Podemos comprobar si nuestros cálculos son verídicos, ya que si sumamos cada diferencia de potencial en cada resistencia, nos debe dar el valor de la fuente principal, es decir:
Podemos comprobar si nuestros cálculos son verídicos, ya que si sumamos cada diferencia de potencial en cada resistencia, nos debe dar el valor de la fuente principal, es decir: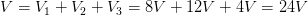
Resistencias en paralelo
Resistencias en Paralelo
Si ya aprendimos a resolver circuitos en serie, ahora es momento de aprender a sumar resistencias en paralelo, para ello debemos seguir ciertas reglas. Entonces:
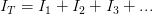 En paralelo la resistencia total del circuito se obtiene con la siguiente fórmula, veamos:
En paralelo la resistencia total del circuito se obtiene con la siguiente fórmula, veamos: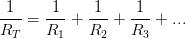 En paralelo la diferencia de potencial es igual a la diferencia de potencial de cada resistencia , es decir:
En paralelo la diferencia de potencial es igual a la diferencia de potencial de cada resistencia , es decir: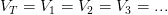
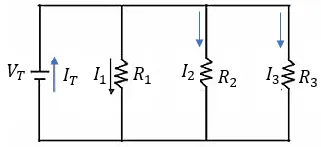
Para entender mejor las características y reglas de las resistencias en paralelo, veamos algunos ejercicios o ejemplos. Ejercicios Resueltos de Suma de Resistencias en Paralelo
Problema 1.- Una resistencia de 4Ω, se conecta en paralelo con otra de 2Ω ¿Cuál es la resistencia total o equivalente del circuito?Solución:
Colocando los datos de nuestro ejercicio:
R1 = 4Ω
R2 = 2Ω
RT = ?
De la fórmula, obtenemos:
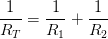 Sumando las resistencias:
Sumando las resistencias: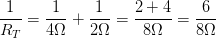 Luego:
Luego: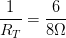 Es decir:
Es decir: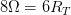
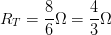 Resultado:Obtenemos un valor de 4/3 Ω
Resultado:Obtenemos un valor de 4/3 Ω
Problema 2.- Una resistencia de 6Ω, 3Ω y 4Ω se conecta en paralelo y una corriente total de 40 A se distribuye entre las tres, ¿cuál es la diferencia de potencial aplicada al circuito?
Solución:
Recolectando nuestros datos, obtenemos
R1 = 6Ω
R2 = 3Ω
R3 = 4Ω
IT = 40A
RT = ?
VT = ?
Para poder calcular la diferencia de potencial de cada componente, debemos al menos conocer al resistencia total.
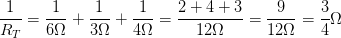 Es decir:
Es decir: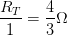
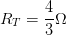 Que sería nuestra resistencia equivalente del circuito, ahora para poder obtener la diferencia de potencial, aplicamos la ley del ohm
Que sería nuestra resistencia equivalente del circuito, ahora para poder obtener la diferencia de potencial, aplicamos la ley del ohm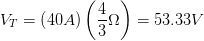
Resultado:Por lo que la diferencia de potencial aplicada al circuito es de 53.33 V
Si ya aprendimos a resolver circuitos en serie, ahora es momento de aprender a sumar resistencias en paralelo, para ello debemos seguir ciertas reglas. Entonces:
- 1 Características de las Resistencias en Paralelo
- 2 Ejercicios Resueltos de Suma de Resistencias en Paralelo
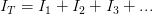 En paralelo la resistencia total del circuito se obtiene con la siguiente fórmula, veamos:
En paralelo la resistencia total del circuito se obtiene con la siguiente fórmula, veamos: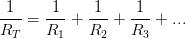 En paralelo la diferencia de potencial es igual a la diferencia de potencial de cada resistencia , es decir:
En paralelo la diferencia de potencial es igual a la diferencia de potencial de cada resistencia , es decir: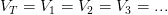

Para entender mejor las características y reglas de las resistencias en paralelo, veamos algunos ejercicios o ejemplos. Ejercicios Resueltos de Suma de Resistencias en Paralelo
Problema 1.- Una resistencia de 4Ω, se conecta en paralelo con otra de 2Ω ¿Cuál es la resistencia total o equivalente del circuito?Solución:
Colocando los datos de nuestro ejercicio:
R1 = 4Ω
R2 = 2Ω
RT = ?
De la fórmula, obtenemos:
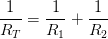 Sumando las resistencias:
Sumando las resistencias: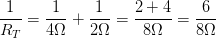 Luego:
Luego: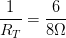 Es decir:
Es decir: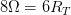
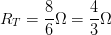 Resultado:Obtenemos un valor de 4/3 Ω
Resultado:Obtenemos un valor de 4/3 ΩProblema 2.- Una resistencia de 6Ω, 3Ω y 4Ω se conecta en paralelo y una corriente total de 40 A se distribuye entre las tres, ¿cuál es la diferencia de potencial aplicada al circuito?
Solución:
Recolectando nuestros datos, obtenemos
R1 = 6Ω
R2 = 3Ω
R3 = 4Ω
IT = 40A
RT = ?
VT = ?
Para poder calcular la diferencia de potencial de cada componente, debemos al menos conocer al resistencia total.
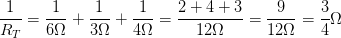 Es decir:
Es decir: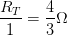
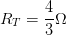 Que sería nuestra resistencia equivalente del circuito, ahora para poder obtener la diferencia de potencial, aplicamos la ley del ohm
Que sería nuestra resistencia equivalente del circuito, ahora para poder obtener la diferencia de potencial, aplicamos la ley del ohm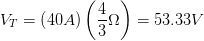
Resultado:Por lo que la diferencia de potencial aplicada al circuito es de 53.33 V
POTENCIA ELÉCTRICA
Potencia Eléctrica

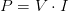 Dónde:
Dónde: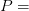 Potencia eléctrica [Watts]
Potencia eléctrica [Watts]
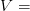 Diferencia de potencial (Voltaje) [Volts = V]
Diferencia de potencial (Voltaje) [Volts = V]
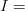 Intensidad de corriente [Ampere = A]
Intensidad de corriente [Ampere = A]
Con base a la ley del ohm, podemos
decir que si: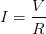 Entonces reemplazando estos valores en nuestra corriente de la primer fórmula, tenemos:
Entonces reemplazando estos valores en nuestra corriente de la primer fórmula, tenemos: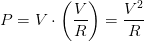
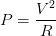 Otra forma de expresarlo, sería si:
Otra forma de expresarlo, sería si: 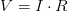 Entonces
Entonces 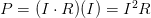
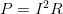 Después de aprender estas fórmulas, para poder adentrarnos al tema, veremos algunos ejemplos.
Después de aprender estas fórmulas, para poder adentrarnos al tema, veremos algunos ejemplos.
Ejemplos resueltos de Potencia Eléctrica Problema 1.- ¿Qué potencia desarrolla un motor eléctrico si se conecta a una diferencia de potencial de 150 volts para que genere una intensidad de corriente de 6 A ?
Solución:
Primero analicemos los datos que el mismo problema nos arroja, en este caso diremos que son los 150 volts del motor y el amperaje que genera.
Datos:
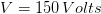
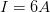
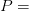 ?
?
Ahora solo basta en reemplazar nuestros datos en la fórmula de potencial eléctrico, para darnos cuenta de cuenta potencia consume el motor.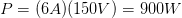 Lo que da un total de 900 Watts de potencia, una cantidad un poquito más de lo equivalente a un caballo de fuerza (hp).
Lo que da un total de 900 Watts de potencia, una cantidad un poquito más de lo equivalente a un caballo de fuerza (hp).
El caballo de fuerza (hp), es una unidad de potencia generalmente usada en los países anglosajones para referirse a la potencia que consumen los motores; sean eléctricos o de combustión, y es equivalente aproximadamente a los 746 Watts
Veamos otro ejemplo más.
Problema 2.- Un motor eléctrico consume una potencia de 1500 W, donde a través de dicho motor existe una diferencia de potencial de 130 volts, ¿Cuál será la corriente a través del motor?
Solución:
Al igual que el ejemplo anterior, es necesario tener consideración de nuestros datos para poder resolver el ejercicio, por ello decimos que:
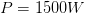
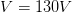
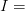 ? De la fórmula:
? De la fórmula: 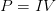
Despejamos a la corriente, y nos queda de la siguiente forma: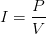 reemplazamos nuestros datos
reemplazamos nuestros datos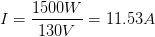 Tenemos que la corriente que pasa a través del motor es de 11.53 Amperes.Ahora veamos otro ejercicio, donde implique de alguna forma un poco más de cálculo algebraico.
Tenemos que la corriente que pasa a través del motor es de 11.53 Amperes.Ahora veamos otro ejercicio, donde implique de alguna forma un poco más de cálculo algebraico.
Problema 3.- Una tostador eléctrico de resistencia R se conecta a una diferencia de potencial V y genera una potencia eléctrica P. Si la diferencia de potencial se reduce a un cuarto. ¿Qué sucede con la potencia generada por el calentador?
Solución:
El problema implica un análisis profundo de lo que ocurre con el tostador eléctrico y a partir de ahí poder sacar una conclusión matemáticas, explicando lo que sucede con la potencia generada por el tostador.
¿Qué datos tenemos?
Sabemos por el problema, que la diferencia de potencial se reduce a un cuarto, entonces lo podemos escribir de la siguiente manera en nuestros datos:
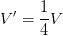 ¿Qué fórmula utilizaremos?Vamos a utilizar una fórmula donde esté implícito la resistencia en la potencia eléctrica, y esa fórmula la colocamos texto arriba de la siguiente forma:
¿Qué fórmula utilizaremos?Vamos a utilizar una fórmula donde esté implícito la resistencia en la potencia eléctrica, y esa fórmula la colocamos texto arriba de la siguiente forma:
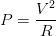 y nuestra incógnita será.
y nuestra incógnita será.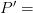 ?
?
Ahora, vamos a reemplazar nuestros datos en la fórmula.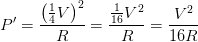
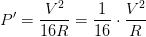 Ahora, hasta este punto debemos observar que en nuestro resultado, estamos obteniendo un octavo de la fórmula original de diferencia de potencial, entonces eso lo podemos reemplazar de la siguiente forma.
Ahora, hasta este punto debemos observar que en nuestro resultado, estamos obteniendo un octavo de la fórmula original de diferencia de potencial, entonces eso lo podemos reemplazar de la siguiente forma.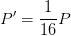 Lo que podemos decir, que la potencia se reduce una dieciseisava parte.¿Fácil no?
Lo que podemos decir, que la potencia se reduce una dieciseisava parte.¿Fácil no?

- 1 ¿Qué es la potencia eléctrica?
- 2 Ejemplos resueltos de Potencia Eléctrica
- 3 Ejercicios Para Practicar de Potencia Eléctrica
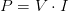 Dónde:
Dónde: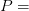 Potencia eléctrica [Watts]
Potencia eléctrica [Watts]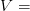 Diferencia de potencial (Voltaje) [Volts = V]
Diferencia de potencial (Voltaje) [Volts = V]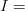 Intensidad de corriente [Ampere = A]
Intensidad de corriente [Ampere = A]Con base a la ley del ohm, podemos
decir que si:
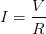 Entonces reemplazando estos valores en nuestra corriente de la primer fórmula, tenemos:
Entonces reemplazando estos valores en nuestra corriente de la primer fórmula, tenemos: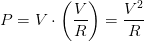
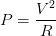 Otra forma de expresarlo, sería si:
Otra forma de expresarlo, sería si: 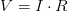 Entonces
Entonces 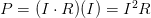
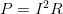 Después de aprender estas fórmulas, para poder adentrarnos al tema, veremos algunos ejemplos.
Después de aprender estas fórmulas, para poder adentrarnos al tema, veremos algunos ejemplos.Ejemplos resueltos de Potencia Eléctrica Problema 1.- ¿Qué potencia desarrolla un motor eléctrico si se conecta a una diferencia de potencial de 150 volts para que genere una intensidad de corriente de 6 A ?
Solución:
Primero analicemos los datos que el mismo problema nos arroja, en este caso diremos que son los 150 volts del motor y el amperaje que genera.
Datos:
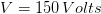
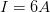
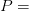 ?
?Ahora solo basta en reemplazar nuestros datos en la fórmula de potencial eléctrico, para darnos cuenta de cuenta potencia consume el motor.
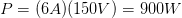 Lo que da un total de 900 Watts de potencia, una cantidad un poquito más de lo equivalente a un caballo de fuerza (hp).
Lo que da un total de 900 Watts de potencia, una cantidad un poquito más de lo equivalente a un caballo de fuerza (hp).El caballo de fuerza (hp), es una unidad de potencia generalmente usada en los países anglosajones para referirse a la potencia que consumen los motores; sean eléctricos o de combustión, y es equivalente aproximadamente a los 746 Watts
Veamos otro ejemplo más.
Problema 2.- Un motor eléctrico consume una potencia de 1500 W, donde a través de dicho motor existe una diferencia de potencial de 130 volts, ¿Cuál será la corriente a través del motor?
Solución:
Al igual que el ejemplo anterior, es necesario tener consideración de nuestros datos para poder resolver el ejercicio, por ello decimos que:
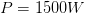
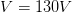
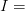 ? De la fórmula:
? De la fórmula: 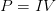
Despejamos a la corriente, y nos queda de la siguiente forma:
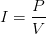 reemplazamos nuestros datos
reemplazamos nuestros datos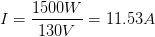 Tenemos que la corriente que pasa a través del motor es de 11.53 Amperes.Ahora veamos otro ejercicio, donde implique de alguna forma un poco más de cálculo algebraico.
Tenemos que la corriente que pasa a través del motor es de 11.53 Amperes.Ahora veamos otro ejercicio, donde implique de alguna forma un poco más de cálculo algebraico.Problema 3.- Una tostador eléctrico de resistencia R se conecta a una diferencia de potencial V y genera una potencia eléctrica P. Si la diferencia de potencial se reduce a un cuarto. ¿Qué sucede con la potencia generada por el calentador?
Solución:
El problema implica un análisis profundo de lo que ocurre con el tostador eléctrico y a partir de ahí poder sacar una conclusión matemáticas, explicando lo que sucede con la potencia generada por el tostador.
¿Qué datos tenemos?
Sabemos por el problema, que la diferencia de potencial se reduce a un cuarto, entonces lo podemos escribir de la siguiente manera en nuestros datos:
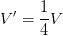 ¿Qué fórmula utilizaremos?Vamos a utilizar una fórmula donde esté implícito la resistencia en la potencia eléctrica, y esa fórmula la colocamos texto arriba de la siguiente forma:
¿Qué fórmula utilizaremos?Vamos a utilizar una fórmula donde esté implícito la resistencia en la potencia eléctrica, y esa fórmula la colocamos texto arriba de la siguiente forma: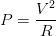 y nuestra incógnita será.
y nuestra incógnita será.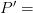 ?
?Ahora, vamos a reemplazar nuestros datos en la fórmula.
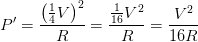
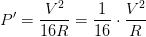 Ahora, hasta este punto debemos observar que en nuestro resultado, estamos obteniendo un octavo de la fórmula original de diferencia de potencial, entonces eso lo podemos reemplazar de la siguiente forma.
Ahora, hasta este punto debemos observar que en nuestro resultado, estamos obteniendo un octavo de la fórmula original de diferencia de potencial, entonces eso lo podemos reemplazar de la siguiente forma.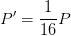 Lo que podemos decir, que la potencia se reduce una dieciseisava parte.¿Fácil no?
Lo que podemos decir, que la potencia se reduce una dieciseisava parte.¿Fácil no? 







