Resistencias en paralelo
Resistencias en Paralelo
Si ya aprendimos a resolver circuitos en serie, ahora es momento de aprender a sumar resistencias en paralelo, para ello debemos seguir ciertas reglas. Entonces:
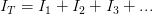 En paralelo la resistencia total del circuito se obtiene con la siguiente fórmula, veamos:
En paralelo la resistencia total del circuito se obtiene con la siguiente fórmula, veamos: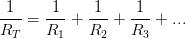 En paralelo la diferencia de potencial es igual a la diferencia de potencial de cada resistencia , es decir:
En paralelo la diferencia de potencial es igual a la diferencia de potencial de cada resistencia , es decir: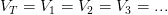
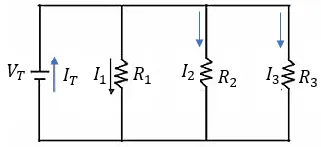
Para entender mejor las características y reglas de las resistencias en paralelo, veamos algunos ejercicios o ejemplos. Ejercicios Resueltos de Suma de Resistencias en Paralelo
Problema 1.- Una resistencia de 4Ω, se conecta en paralelo con otra de 2Ω ¿Cuál es la resistencia total o equivalente del circuito?Solución:
Colocando los datos de nuestro ejercicio:
R1 = 4Ω
R2 = 2Ω
RT = ?
De la fórmula, obtenemos:
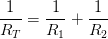 Sumando las resistencias:
Sumando las resistencias: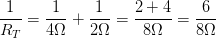 Luego:
Luego: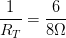 Es decir:
Es decir: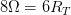
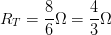 Resultado:Obtenemos un valor de 4/3 Ω
Resultado:Obtenemos un valor de 4/3 Ω
Problema 2.- Una resistencia de 6Ω, 3Ω y 4Ω se conecta en paralelo y una corriente total de 40 A se distribuye entre las tres, ¿cuál es la diferencia de potencial aplicada al circuito?
Solución:
Recolectando nuestros datos, obtenemos
R1 = 6Ω
R2 = 3Ω
R3 = 4Ω
IT = 40A
RT = ?
VT = ?
Para poder calcular la diferencia de potencial de cada componente, debemos al menos conocer al resistencia total.
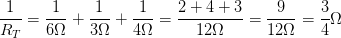 Es decir:
Es decir: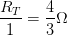
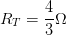 Que sería nuestra resistencia equivalente del circuito, ahora para poder obtener la diferencia de potencial, aplicamos la ley del ohm
Que sería nuestra resistencia equivalente del circuito, ahora para poder obtener la diferencia de potencial, aplicamos la ley del ohm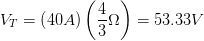
Resultado:Por lo que la diferencia de potencial aplicada al circuito es de 53.33 V
Si ya aprendimos a resolver circuitos en serie, ahora es momento de aprender a sumar resistencias en paralelo, para ello debemos seguir ciertas reglas. Entonces:
- 1 Características de las Resistencias en Paralelo
- 2 Ejercicios Resueltos de Suma de Resistencias en Paralelo
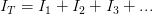 En paralelo la resistencia total del circuito se obtiene con la siguiente fórmula, veamos:
En paralelo la resistencia total del circuito se obtiene con la siguiente fórmula, veamos: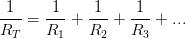 En paralelo la diferencia de potencial es igual a la diferencia de potencial de cada resistencia , es decir:
En paralelo la diferencia de potencial es igual a la diferencia de potencial de cada resistencia , es decir: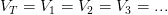

Para entender mejor las características y reglas de las resistencias en paralelo, veamos algunos ejercicios o ejemplos. Ejercicios Resueltos de Suma de Resistencias en Paralelo
Problema 1.- Una resistencia de 4Ω, se conecta en paralelo con otra de 2Ω ¿Cuál es la resistencia total o equivalente del circuito?Solución:
Colocando los datos de nuestro ejercicio:
R1 = 4Ω
R2 = 2Ω
RT = ?
De la fórmula, obtenemos:
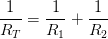 Sumando las resistencias:
Sumando las resistencias: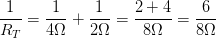 Luego:
Luego: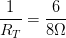 Es decir:
Es decir: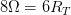
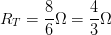 Resultado:Obtenemos un valor de 4/3 Ω
Resultado:Obtenemos un valor de 4/3 ΩProblema 2.- Una resistencia de 6Ω, 3Ω y 4Ω se conecta en paralelo y una corriente total de 40 A se distribuye entre las tres, ¿cuál es la diferencia de potencial aplicada al circuito?
Solución:
Recolectando nuestros datos, obtenemos
R1 = 6Ω
R2 = 3Ω
R3 = 4Ω
IT = 40A
RT = ?
VT = ?
Para poder calcular la diferencia de potencial de cada componente, debemos al menos conocer al resistencia total.
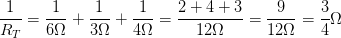 Es decir:
Es decir: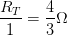
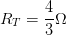 Que sería nuestra resistencia equivalente del circuito, ahora para poder obtener la diferencia de potencial, aplicamos la ley del ohm
Que sería nuestra resistencia equivalente del circuito, ahora para poder obtener la diferencia de potencial, aplicamos la ley del ohm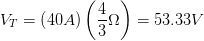
Resultado:Por lo que la diferencia de potencial aplicada al circuito es de 53.33 V
